As Arteiras - CSJB

A Proporção Áurea

Por mais de 500 anos antes de Cristo, os gregos (pitagóricos), vem estudando as relações entre os segmentos de um pentagrama. Determinaram um número que desempenhava um importante papel na geometria, na estética, nas artes, na arquitetura e na biologia. Este número é chamado de número áureo (número de ouro) ou razão (secção) áurea. A razão áurea, além de um conceito matemático, é uma expressão de harmonia e beleza.

 Os antigos gregos avaliavam essa harmonia nos seres vivos e não-vivos, buscando em suas dimensões uma proporção que se aproximasse da razão áurea. Um segmento de reta ou linha dividida na Razão Áurea é uma das primeiras situações que aparece quando se pesquisa sobre a Razão Áurea.

O estudo da Razão Áurea pode se começar por um segmento de reta qualquer, que podemos imaginar que esteja dividido de tal forma que resulte em um segmento maior e outro segmento menor. A Razão Áurea ocorre quando o segmento menor dividido pelo maior é igual ao maior dividido pelo segmento todo.

Este processo nos leva cada vez mais próximos do valor de 1,6180339.

É surpreendente que a razão áurea esteja intimamente relacionada com a chamada seqüência de Fibonacci.0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,... 

Vamos verificar que Fibonacci conseguiu provar que um número dividido pelo anterior aproximava do número de ouro.

3.2. O NÚMERO DE OURO

O número de ouro não é mais do que um valor numérico cujo valor aproximado é1,6180339... Este número irracional é considerado por muitos o símbolo da harmonia. A escola grega de Pitágoras estudou e observaram muitas relações e modelos numéricos que apareciam na natureza, beleza, estética, harmonia musical e outros, mas provavelmente a mais importante é a razão áurea, razão divina ou proporção divina. Se quiséssemos dividir um segmento AB em duas partes, teríamos uma infinidade de maneiras de fazê-lo. Existe uma, no entanto, que parece ser mais agradável à vista, como se traduzisse uma operação harmoniosa para os nossos sentidos.Formulou-se, o seguinte princípio: “Para que um todo dividido em duas partes desiguais pareça belo do ponto de vista da forma, deve apresentar à parte menor e a maior a mesma relação que entre esta e o todo.”
A história deste enigmático número perde-se na antiguidade. No Egito as pirâmides de Gizé foram construídas tendo em conta a razão áurea.

Outro exemplo da proporção áurea na antiguidade é o Papiro de Rhind (Egípcio) ouAhmes e também o Parthenon Grego, templo representativo do século de Péricles contém a razão de ouro no retângulo que contem a fachada.

Assim como o Parthenon, também podemos citar como uma maravilha que possua a razão áurea, o Taj Mahal, edificação maravilhosa, construída baseada na razão áurea, objeto de estudo de vários cientistas, matemáticos,arquitetos, em toda parte frontal podemos localizar a razão áurea .

LEONARDO DA VINCI  E O NÚMERO DE OURO

A perfeição dos desenhos de Leonardo da Vinci nos mostra os seus conhecimentos matemáticos, como a utilização da razão áurea para uma garantia de uma perfeição, beleza e harmonia única de suas obras. Ele usou exaustivamente os seus conhecimentos de matemática, principalmente o número de ouro em suas obras de arte. Um exemplo é a tradicional representação do homem em forma de estrela de cinco pontas de Leonardo, a qual foi inspirada no pentágono regular e estrelado inscrita na circunferência.

Podemos verificar que na era renascentista, a perfeição e a beleza eram bastante exploradas em pinturas, a razão áurea pode ser encontrada em diversas obras, Salvador Dali que pintou O Sacramento da Ultima Ceia. Podemos verificar o Retângulo de Ouro quando na Monalisa .

Ao desenharmos um retângulo à volta da face o retângulo resultante é um Retângulo de Ouro;
Dividirmos este retângulo por uma linha que passe nos olhos, o novo retângulo obtido também é de Ouro.

O NÚMERO DE OURO NA NATUREZA

Podemos observar também algumas aplicações do número de ouro na natureza. Os números de Fibonacci podem ser usados para caracterizar diversas propriedades na natureza. O modo como as sementes estão em certa ordem no centro de diversas flores é um desses exemplos.

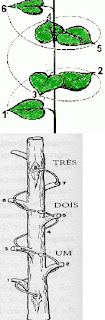
O retângulo de ouro pode ser encontrado na concha do Nautilus, veja o esquemaabaixo, que mostra o espiral da concha limitado pelo retângulo áureo. Também encontramos aespiral no rabo do camaleão. A seqüência 1, 1, 2, 3, 5, 8, 13,..., correspondente aos lados dosquadrados que montam essa espiral.

A MÚSICA E A RAZÃO ÁUREA

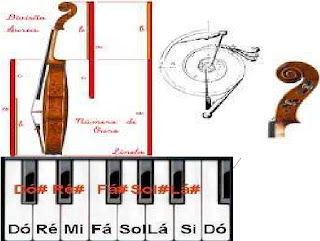
Na música, existem artigos que relacionam as composições de Mozart, Bethoveen (Quinta Sinfonia), Schubert e outros com a razão áurea. Pode-se verificar na figura que até mesmo a construção de instrumentos, como exemplo o violino, está relacionado com a proporção áurea.